All physical quantities do not have unit, quantities which are represented as
the ration of the two same physical quantities do not have any unit.
Example: Refractive Index (μ) =velocity of light in vacuum/velocity of light in
medium
Specific Gravity = Density of the substance/density of water
Generally we have three fundamental physical quantities
1. Mass
2. Length
3. Time
They are called fundamental because they do not require the help of other
physical quantity for their representation.
Most of the other physical quantities can be represented in terms of these
physical quantities. When a physical quantity is represented in terms of
fundamental quantities it is known as dimension of that physical quantity.
Units: Generally we have two types
of units
1. Fundamental Unit
2. Derived Unit
Fundamental Unit: The units of fundamental quantities are known as fundamental
units.
Derived Unit: The units of all other physical quantities which can be derived
from the fundamental units are known as derived units.
System of Units: We have the following system of fundamental units
|
Sr No.
|
System
|
Length
|
Mass
|
Time
|
Current
|
|
1
|
F.P.S
|
Foot
|
Pound
|
Second
|
|
|
2
|
C.G.S
|
Centimetre
|
Gram
|
Second
|
|
|
3
|
M.K.S
|
Meter
|
Kilogram
|
Second
|
|
|
4
|
M.K.S.A
|
Meter
|
Kilogram
|
Second
|
Ampere
|
|
5
|
SI
|
Meter
|
Kilogram
|
Second
|
Ampere
|
Angle: Radian, Solid Angle : Ste-Radian, Temperature : Kelvin, Luminous
Intensity: Candela
The MKSA was un-rational system later MKSA was rationalised by introducing
special constant and is known as International System of Unit (SI unit).
The seven fundamental
units are:
-
meter(m), is the length of the path traveled by light in vacuum in an interval
of 1/299 792 458 seconds;
-
second(s), is the duration of 9,192,631,770 periods of the radiation
corresponding to the transition between two hyperfine levels of the ground state
of the cesium 133;
-
kilogram(kg), is the unit of mass; it equal to the mass of the international
prototype of the kilogram. This prototype, made
of platinum-iridium, is kept at Sevres in 1889;
-
ampere(A), is the intensity of a constant electric current which, if maintained
in two straight parallel conductors of infinite length, of negligible circular
cross section, placed at a distance of one meter in vacuum, would produce
between these conductors a force equal to 2 x 10-7 newton per meter of length;
-
kelvin(K), unit of thermodynamic temperature, is the fraction 1/273.16 of the
thermodynamic temperature of the triple point of water;
-
mole(mol), is the amount of substance of a system which contains as many
elementary entities as there are atoms in 0.012 kg of carbon 12. When the mole
is used, the elementary entities must be specified; may be atoms, molecules,
ions, electrons, other particles, or specified groups of such particles;
-
candela(cd), is the luminous intensity, in a given direction, of a source that
emits monochromatic radiation of frequency 540×1012 hertz and intensity in that
direction of 1/683 watt per steradian.
Derived Unit: To find derived unit of a physical quantity we must write the
dimension of that physical quantity.
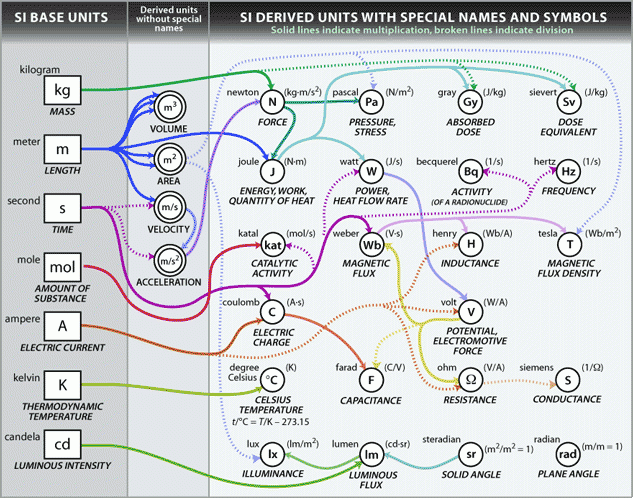
1.
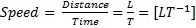
Unit: CGS = cm sec-1
SI=m
sec-1
2.

Unit: CGS = cm sec-2
SI=m
sec-2
3.

Unit: CGS = gm.cm. sec-2 = 1 dyne
SI=kg.m.
sec-2 = 1 Newton
4.

Unit: CGS = gm.cm2. sec-2 = 1 erg
SI=kg.m2.
sec-2 = 1 Joule
5.
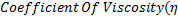 )
)
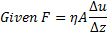
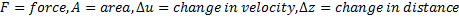
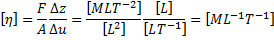
Unit: CGS=gmcm-1Sec-1 = ( 1 Poise )
SI: Kg m-1S-1
6.
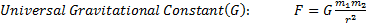
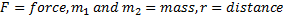
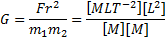
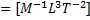
Use of Dimension
A.
From the dimension of physical quantity we can convert from
one system of unit to other.
1.
Example: Dyne and
Newton both are units of force one in C.G.S and other is in SI respectively
find 1 Dyne = ? Newton
We know

In C.G.S
1 Dyne = 1 gm.1cm.1sec-2
1 Dyne = 10-3 Kg.10-2m.1 sec-2
1 Dyne = 10-5 Newton
Or
1
Newton = 105 Dyne
2.
Both Erg and Joule are units of Work find 1 Erg = ? Joule
We know
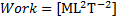
In CGS = gm.cm2. sec-2 = 1 erg
SI=kg.m2.
sec-2 = 1 Joule
1 Erg = 1gm.cm2. sec-2
1 Erg = 10-3Kg.(10-2)2m2. sec-2
1 Erg = 10-7 Joule
1
Joule = 10-7 Erg
3.
Vlaue of G = 6.667 X 10-8
CGS Unit. Find the value in S.I Unit
We Know that [G]
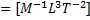
In C.G.S
G = 6.667 X 10-8 gm-1 cm3 sec-2
G = 6.667 X 10-8(10-3)-1 Kg-1
(10-2)3m3 sec-2
G = 6.667 X 10-11 S.I unit
B.
By writing dimension we can check whether the given equation
is correct or not?
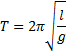
Dimension of L.H.S = [T]
Dimension of R.H.S =
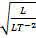 = [T]
= [T]
We found that the dimension of
both sides of this equation is same hence above equation is dimensionally
correct.